חוסר יכולת אפידמיולוגית של יעילות חיסונים של CDC

מעת לעת במהלך מגיפת Covid-19, הצוות המדעי של CDC השתמש בנתוני המחקרים הזמינים שלהם כדי להעריך את היעילות של גרסאות עדכניות או עדכניות של חיסוני Covid-19 כדי להפחית את הסיכון להיבדק חיובי ל-Covid-19. אמנם העובדה של "בדיקה חיובית" הייתה מעט שנויה במחלוקת בגלל מספרי הסף הסודיים של PCR Ct המעורבים שאיפשרו לאנשים לא מדבקים עם Covid-19 לא מזוהה מכמה שבועות בעבר להישאר חיוביים למבחן, המטרה שלי כאן היא להמחיש השיטות האפידמיולוגיות הבעייתיות של CDC שניפחו באופן משמעותי את אחוזי יעילות החיסון שעליהם דיווחו.

מחקרים אפידמיולוגיים מבוקרים מתחלקים לשלושה ולשלושה עיצובי מחקר בסיסיים בלבד. או שנדגמים מדגם כולל של נבדקים, וכל נבדק מוערך הן עבור סטטוס המקרה והן עבור מצב החשיפה הקודם - זהו מחקר חתך - או שעוקבים אחר מדגם של אנשים חשופים ומדגם של אנשים לא נחשפים כדי לראות מי הופך ל- מקרה ומי מתקבל ביקורת - מחקר עוקבה - או מדגם של מקרים ומדגם של בקרות, וכל נבדק מוערך לגבי מצב חשיפה בעבר - זהו מחקר מקרה-ביקורת. אם מחקר עוקבה כולל חלוקה אקראית של הנבדקים לאלו שנחשפו ולא נחשפו, זהו מחקר אקראי מבוקר (RCT), אך תכנון המחקר הוא עדיין עוקבה.

במחקר חתך ומחקר עוקבה, ה הסיכון ניתן להעריך את התוצאה של עניין (כלומר, להיות נבדק במקרה, כאן, בדיקה חיובית) עבור האנשים הנחשפים לפי מספר המקרים בין הנחשפים חלקי המספר הכולל שנחשפו. באופן דומה לבלתי חשופים. מה שמעניין, ההשוואה בין שני הסיכונים הללו, הסיכון היחסי (RR), היא הסיכון בחשיפה חלקי הסיכון בבלתי חשוף. ה-RR מעריך עד כמה הסיכון גרוע יותר בקרב הנחשפים בהשוואה לבלתי נחשפים. עבור חיסון או חשיפה אחרת המורידה את הסיכון, ה-RR יהיה פחות מ-1.0.

מחקרי חתך וקוהורט, לפי עיצובי הדגימה שלהם, מאפשרים להעריך את ה-RR מהנתונים שלהם. עם זאת, מחקרי בקרת מקרה אינם מאפשרים להעריך את סיכוני התוצאה, מכיוון ששינוי המספר היחסי של מקרים שנדגמו לעומת בקרות משפיע על הערכות הסיכון. במקום זאת, מחקרי מקרה-ביקורת מאפשרים להעריך את הסיכויים של התוצאה, לא הסיכון. לדוגמה, סיכוי של 2:1 לקרות אירוע. ערך זה אינו מושפע מעיצוב הדגימה. במחקרי מקרה-ביקורת, הסיכויים היחסיים (או יחס הסיכויים, OR) של התוצאה נאמדים לפי סיכויי התוצאה בקרב הנחשפים, חלקי הסיכויים בקרב הלא-נחשפים.

עבור חיסון, יעילותו מוערכת ב-1.0 - RR. עבור נתוני מחקר מקרה-ביקורת שמעריכים רק את OR לא את RR, מתי ה-OR מקרוב את ה-RR במדויק מספיק כדי להיות מוחלף בנוסחה זו? לשאלה זו יש היסטוריה אפידמיולוגית מפורטת מעבר להיקף הנוכחי, אך במובן הפשוט ביותר, ה-OR מתקרב ל-RR כאשר באוכלוסיה, מקרים נדירים בהשוואה לביקורות.

עכשיו ל-CDC ולשגיאות האפידמיולוגיות השיטתיות שלו. בניתוח שנערך לאחרונה, לינק-גלס ועמיתיו דגמו בסך הכל 9,222 אנשים זכאים דמויי Covid-19 סימפטומטיים המבקשים בדיקת Covid-19 בבתי המרקחת CVS ו-Walgreen Co. במהלך ה-21 בספטמבר 2023 עד ה-14 בינואר 2024. הם העריכו את מצב החיסון הקודם של כל פרט, כמו גם חיוביות של תוצאת הבדיקה. בהגדרה, זהו מחקר חתך, מכיוון שלא נדגמו מספרים בודדים של מקרים ובקרות, או מספרים בודדים של חשופים (מחוסנים) ובלתי-נחשפים (לא מחוסנים). נדגמו רק המספר הכולל של הנבדקים.

עם זאת, החוקרים העריכו את ה-OR ולא את ה-RR מנתונים אלה, על ידי שימוש בשיטת ניתוח סטטיסטי הנקראת רגרסיה לוגיסטית המאפשרת להתאים את ה-OR לגורמים מבלבלים אפשריים שונים. אין שום פסול בשימוש ברגרסיה לוגיסטית וקבלת ORs משוערים בכל עיצוב מחקר; הבעיה היא שימוש בערך OR במקום RR בנוסחת יעילות החיסון 1.0 - RR. מכיוון שתכנון המחקר היה חתך רוחב, החוקרים יכלו לבחון את התרחשות המקרים היחסית באוכלוסיה לפי המספרים הנדגמים שלהם, אך נראה שהם לא עשו זאת. למעשה, המקרים כללו 3,295 מתוך סך 9,222 הנדגמים, 36%, וזה לא כמעט קטן מספיק כדי להשתמש ב-OR כתחליף ל-RR. זה נכון הן בקרב הנבדקים שנחשפו (25%) והן בקרב הלא נחשפים (37%).

עם זאת, ניתן לקבל מושג גס עד כמה הנחה רעה זו השפיעה על יעילות החיסון הכוללת הנטענת של המחברים של 54%. המספרים הרלוונטיים של נושאים, המוצגים בטבלה שלהלן, מצוינים בטבלאות 1 ו-3 של מאמר Link-Gelles. חישוב ה-RR מנתונים גולמיים אלה הוא פשוט. הסיכון אצל המחוסנים הוא 281/1,125 = 25%; אצל הלא מחוסנים זה 3,014/8,097 = 37%. ה-RR הוא היחס בין שני אלה, 25%/37% = 0.67, ולכן יעילות החיסון בהתבסס על נתונים גולמיים אלו תהיה 1.0 - 0.67 = 0.33 או 33%.

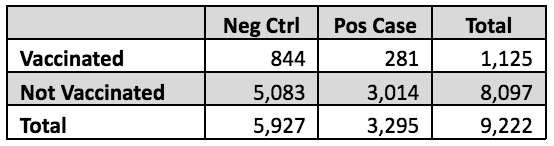
באופן דומה ניתן להעריך את ה-OR מנתונים גולמיים אלה כ-0.56, שאם נעשה בהם שימוש בנוסחת יעילות החיסון ייתן יעילות של 44%, שונה במידה ניכרת מיעילות 33% כפי שהוערכה כראוי על ידי שימוש ב-RR.

עם זאת, Link-Gelles et al. השתמשו ב-OR המתואם = 0.46 כפי שהתקבל מניתוח הרגרסיה הלוגיסטית שלהם. זה שונה מ-OR = 0.56 ללא התאמה בפקטור של 0.46/0.56 = 0.82. אנו יכולים להשתמש במקדם ההתאמה הזה, 0.82, כדי להעריך מה היה ה-RR הגולמי לו היה מותאם על ידי אותם גורמים: 0.67*0.82 = 0.55. מספרים אלו מוצגים בטבלה שלהלן, ומוכיחים כי יעילות החיסון הנכונה היא כ-45%, לא ה-54% הנטען, ופחות מהרמה הנומינלית הרצויה של 50%.

כאפידמיולוג, לא ברור לי מדוע עמיתיי ב-CDC היו משתמשים בטעות ב-OR כתחליף ל-RR כאשר ההנחה הנדרשת להחלפה זו לא התקיימה והייתה ניתנת לבדיקה בקלות בנתונים שלהם. הם עשו את השגיאה הזו במקום אחר (Tenforde et al.) שם הוא גם עשה הבדל ניכר ביעילות החיסון, כ-57% לעומת 82% הנטען. אולי המחברים חשבו שהשיטה היחידה הזמינה להתאמה למשתנים מבלבלים מרובים היא רגרסיה לוגיסטית המשתמשת ב-OR, אבל רגרסיה בסיכון יחסי להתאמת ה-RR זמינה מזה זמן רב בחבילות ניתוח סטטיסטי מסחרי שונות והיא מיושמת בקלות (עַרעָר).

נראה לי מפתיע שככל הנראה אף אחד מיותר מ-60 המחברים בין המאמרים של Link-Gelles ו-Tenforde זיהה שעיצוב הדגימה של המחקרים שלהם היה חתך רוחב, לא בקרת מקרה, ולפיכך הפרמטר המתאים לשימוש לאומדן יעילות החיסון הייתה ה-RR ולא ה-OR, וכי הנחת המחלה הנדירה להחלפת ה-OR ב-RR לא התקיימה בנתונים שלהם. לפיכך, מחקרים אלה העריכו באופן משמעותי את יעילות החיסון האמיתית בתוצאות שלהם. זה לא נושא אקדמי גרידא, מכיוון שהחלטות מדיניות בריאות הציבור של CDC יכולות להיגזר מתוצאות שגויות כמו אלה.